最长递增子序列
说明
这道题并不是 leetcode 上面的原题,是作者在阅读 Vue 核心 diff 算法的文章中涉及到的,觉得还挺有难度,所以就研究一下。这个问题的应用场景在于 Vue 3 的核心 Diff 算法中DOM 的移动方式。在经过 Diff 算法之前的预处理步骤以及判断 DOM 节点是否需要移动之后,可以拿到剩下的新节点列表的每一个节点在旧节点列表对应的索引用数组 source 存储,如果新节点在旧节点列表中不存在则表示是新增节点,其索引为-1,直接添加即可。
该算法中 DOM 移动方式的原理大概就是:找出 source 数组中的最长递增子序列 lis,如果从后向前遍历剩余的新节点列表,如果该节点列表的索引值在 lis 中,则认为该节点无需移动,否则需要移动。
题目描述
给出一个数组,找出其最长递增子序列,返回子序列对应的索引(结果不唯一,找出一个就可以)
示例
输入:[0, 8, 4, 12, 2, 10]
输出:[0, 4, 5]解题思路
将整个问题拆分成子问题:通过将序列进行拆分更短的子序列,优先求解长度更短的序列的最长递增子序列,进而求得原序列的最长递增子序列。
首先,我们为原序列中的每个数字分配一个格子,并且这些格子填充 1 作为初始值(格子中的数字表示所对应的数字为开头的递增子序列的最大长度):
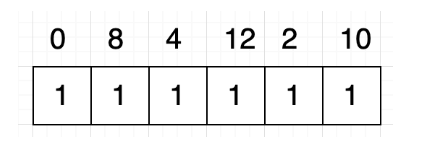
然后,我们从后向前依次求取以当前元素开头的序列的最长递增子序列的长度。按照上图可知,我们第一步应该求[10]这个序列最长递增子序列的长度,很明显就是 1。接下来我们来求以 2 开头的序列也就是[2, 10]的最长递增子序列的长度。这个改怎么求呢?虽然通过肉眼观察一眼就能看出序列[2, 10]对应的最长递增子序列的长度是 2,但是转化为算法,我们是通过比较 2 和 10 的关系,因为 2<10,那 2 对应的格子里的数应该是 10 对应的格子中数加上 1。因为 2<10,也就是说在以 10 开头的序列前面加上 2 之后,仍然满足递增的关系,所以以 2 开头的序列的最长递增子序列的长度=以 10 开头的最长自增子序列的长度+1,所以,结果就是:
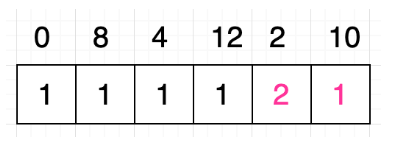
接下来,将问题扩展到求[12, 2, 10]的最长递增子序列。我们将 12 与 2 和 10 进行比较,发现 12 比 2 和 10 都大,也就是说 12 和以 2 或者 10 都无法构成递增序列,所以 12 对应的格子数应该还是 1。下一步将问题扩展到[4, 12, 2, 10],同样的用 4 依次和 12,2,10 进行比较,发现满足 4<12,4<10,所以我们找到 12 和 10 对应的格子数分别加 1 然后取其中的最大值。完成之后结果如下:
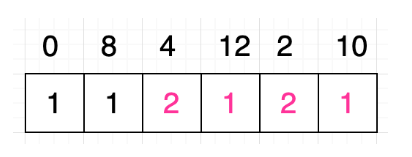
后面我们对于 8 和 0 做同样的处理然后得到的结果如下:
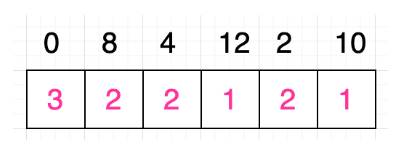
如上图所示,现在所有格子的值都已经更新完毕,接下来我们要做的就是根据这些值,找到整个序列的最长递增子序列。那么应该如何寻找呢?很简单,实际上这些格子中的最大值就代表了整个序列的递增子序列的最大长度,上图中数字 0 对应格子的值为 3,是最大值,因此原序列的最长递增子序列一定是以数字 0 开头的,接着选取格子数为 2 对应的元素,然后选择 1 对应的元素。当然,最长递增子序列并不唯一,所以本文只是从小到大取第一个子序列。
注意:原文中的代码最后取子序列的方法是从原序列末尾开始从格子数由小取到大。但是这种方法存在问题,比如当原序列为[0, 8, 4, 12, 24, 2, 10]时,其对应的格子为:[4, 3, 3, 2, 1, 2, 1],如果按照原文的方法从序列末尾按照格子数从小到大的取,会取成[0, 4, 2, 10],这并不是递增序列,所以需要注意一下。
代码
function lis(seq) {
const valueToMax = {};
for (let num of seq) {
valueToMax[num] = 1;
}
let len = seq.length,
maxLen = 1;
let i = len - 1;
let last = seq[i],
prev = seq[i - 1];
while (i >= 1) {
let j = i;
while (j < len) {
last = seq[j];
if (prev < last) {
const currentMax = valueToMax[last] + 1;
valueToMax[prev] =
valueToMax[prev] === 1
? currentMax
: currentMax > valueToMax[prev]
? currentMax
: valueToMax[prev];
maxLen = maxLen > valueToMax[prev] ? maxLen : valueToMax[prev];
}
j++;
}
i--;
last = seq[i];
prev = seq[i - 1];
}
const res = [];
for (let i in seq) {
const n = seq[i];
if (maxLen < 0) break;
if (valueToMax[n] === maxLen) {
res.push(i);
maxLen--;
}
continue;
}
return res;
}测试结果:
const seq = [0, 3, 8, 5, 4, 12, 15, 2, 10];
console.log(lis(seq));
// [ 0, 1, 2, 5, 6 ]
