10. 正则表达式匹配
题目描述
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*‘ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*‘ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
说明:
- s 可能为空,且只包含从 a-z 的小写字母。
- p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例
- 示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。- 示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。- 示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。- 示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。- 示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false解题思路
方法一:JS 构建正则表达式
/**
* @param {string} s
* @param {string} p
* @return {boolean}
*/
var isMatch = function (s, p) {
return new RegExp("^" + p + "$").test(s);
};方法二:动态规划
由题意可知,s 为待匹配字符串,而 p 则为待匹配的正则表达式,正则表达式中”.”表示匹配一个任意字符,”*“则是量词表示其前面的一个字符可以出现 0 次或多次。
本题的重点是遇到”*“该怎么处理,举个小例子:
假设 s=ab,p=a*b*,那么毫无疑问 s.match(p)是成立的。但是如果将 p 变成 a*b*c,那么这就是不成立的,因为 s 并没有 c,如果将 p 再加一个*变成 a*b*c*,那么匹配又会变成立,因为 c 这个时候可以匹配为 0 个。
所以匹配到*号的时候具体到代码上逻辑如下:
if (p.charAt(i) === "*") {
// 当p[i]="*"时,可以使p[i]和p[i-1]位置的字符不出现,也就是说只有匹配到p[i-2]时为true时,匹配到p[i]处时才能匹配成功即p[i]=p[i-2],又因为我们的状态矩阵是在p和s前面都加了一个空字符之后建立的,所以上述情况dp状态矩阵对应p的下标应该加上1(0下标对应的是"",1下标对应的是p的0下标对应的字符匹配情况,后面以此内推……)
dp[i + 1] = dp[i - 1];
}以上的逻辑思路就是当匹配到 a*b*c*中时,判断最后一个*是否匹配成立只需要看第 2 个*,即 a*b*是否匹配,如果匹配那么 a*b*c*也是成立的,假如 s 换成是 ad,那么走到 a*b 的时候就已经不匹配了,经过状态转移 a*b*c*也不会匹配,所以可以使用动态规划来解题。
第一步:建立状态转移数组
创建一个二维数组 dp[s.length+1][p.length+1],其中每个值先初始化置为 false,首先将 dp[0][0]置为 true。为什么这里要将其置为 true 呢?原因如下图所示: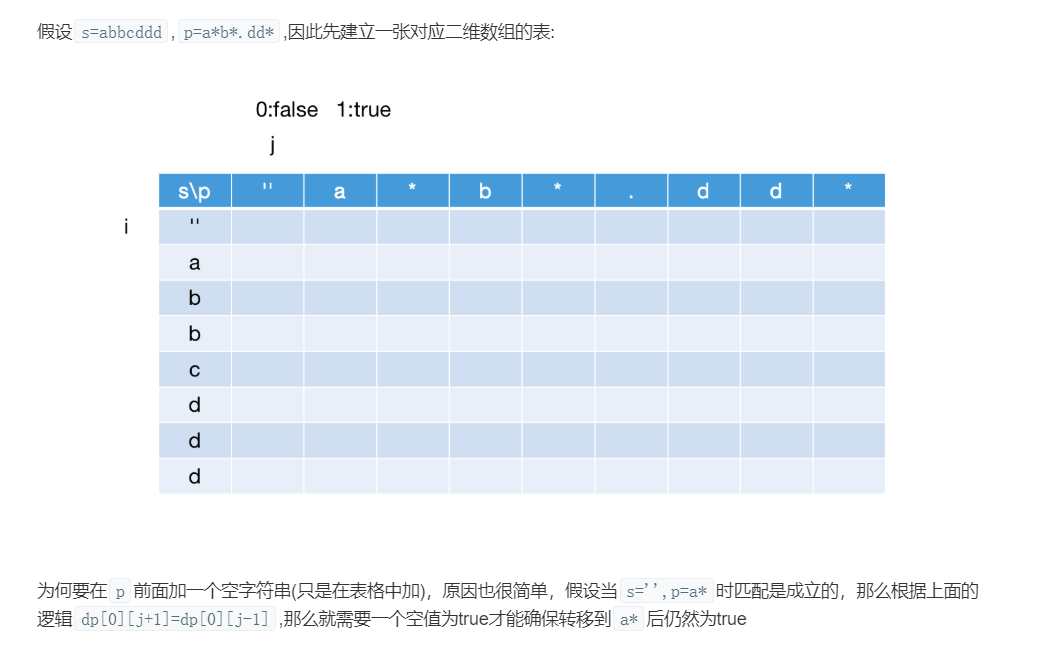
将 s 先设为空字符串,来获得一些简单的匹配结果,如下图所示: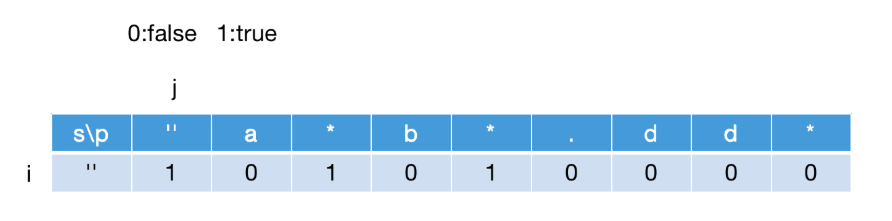
注意:上图中 p[j]=”.”时也为 false,这是因为”.”可以匹配任意字符但是不能为为空,因此也为 false。上诉步骤代码如下:dp[0][0] = true; for (let i = 1; i < p.length; i++) { if (p[i] === "*") { dp[0][i + 1] = dp[0][i - 1]; } }注意:dp[i][j]表示的是 s 的前[i-1]个字符与 p 的前[j-i]个字符的匹配结果
第二步:匹配状态转移
在 dp[0]全部赋值后开始对字符串 s 和模式字符串 p 进行逐一匹配,那么匹配过程一共会碰到三种情况:- p[j]为普通字符时:
如果 s[i]===p[j],那么 dp[i+1][j+1]=dp[i][j]; - p[j]为’.’时,这时可以把’.’看成是一个任意字符,此时可以看作是 s[i]===p[j]这种情况,因此 dp[i+1][j+1]=dp[i][j];
- p[j]为’*‘时,此时又可以分几种情况:
- p[j-1] !== s[i] && p[j-1] !== “.”时,此时 p[j]的匹配情况取决于 p[j-2]的匹配情况,即 dp[i+1][j+1]=dp[i+1][j-1]
- p[j-1] === s[i]时,因为 p[j]=”*“,这里可以根据 p[j-1]这个字符可以连续匹配的次数 n 分三种情况:
- n=0,也就是说 p[j-1]这个字符不出现,情况同上,此时 dp[i+1][j+1]=dp[i+1][j-1];
- n=1,也就是此时 p[j-1]这个字符出现 1 次,此时 dp[i+1][j+1]=dp[i+1][j];
- n>=2,也就是此时 p[j-1]这个字符出现多次,此时 dp[i+1][j+1]=dp[i+1][j-1] 和 dp[i+1][j+1]=dp[i+1][j]都有可能为 false,此时的情况可以通过 dp[i+1][j+1]=dp[i][j+1]来判断;
上述情况归纳可得:
if (p[j - 1] !== s[i] && p[j - 1] !== ".") { dp[i + 1][j + 1] = dp[i + 1][j - 1]; } else { dp[i + 1][j + 1] = dp[i + 1][j - 1] || dp[i + 1][j] || dp[i][j + 1]; }- p[j]为普通字符时:
代码
/**
* @param {string} s
* @param {string} p
* @return {boolean}
*/
var isMatch = function (s, p) {
let dp = new Array(s.length + 1)
.fill(false)
.map(() => new Array(p.length + 1).fill(false));
dp[0][0] = true;
for (let i = 0; i < p.length; i++) {
if (p[i] === "*") {
dp[0][i + 1] = dp[0][i - 1];
}
}
for (let i = 0; i < s.length; i++) {
for (let j = 0; j < p.length; j++) {
if (s[i] === p[j] || p[j] === ".") {
dp[i + 1][j + 1] = dp[i][j];
}
if (p[j] === "*") {
if (p[j - 1] !== s[i] && p[j - 1] !== ".") {
dp[i + 1][j + 1] = dp[i + 1][j - 1];
} else {
dp[i + 1][j + 1] = dp[i + 1][j - 1] || dp[i + 1][j] || dp[i][j + 1];
}
}
}
}
return dp[s.length][p.length];
};
