每天一道leetcode(Day 11)

面试题 13. 机器人的运动范围

题目描述

地上有一个 m 行 n 列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如，当 k 为 18 时，机器人能够进入方格 [35, 37] ，因为 3+5+3+7=18。但它不能进入方格 [35, 38]，因为 3+5+3+8=19。请问该机器人能够到达多少个格子？

示例

• 示例 1：

输入：m = 2, n = 3, k = 1
输出：3

• 示例 2：

输入：m = 3, n = 1, k = 0
输出：1

• 提示：

1 <= n,m <= 100
0 <= k <= 20

解题思路

解题主要思路是 广度优先搜索 或者 深度优先搜索 ，一张图示例可以走通的位置，

m=20, n=15, k=9 的情况(转自 leetCode)，绿色区域表示能走的地方，红色区域表示不能走的地方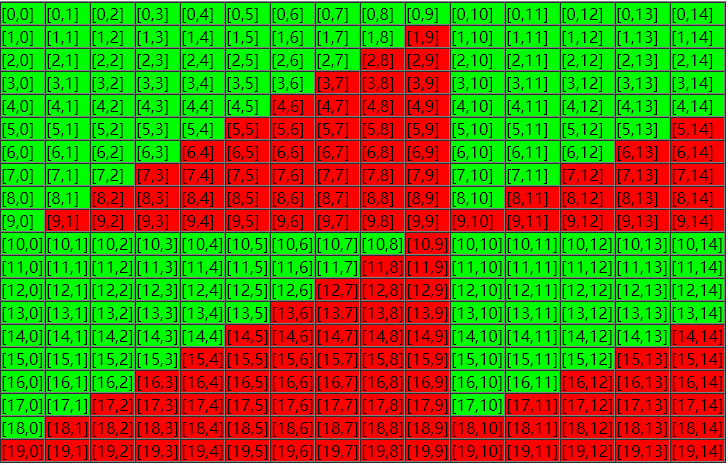

由图中可以看出，右下角存在绿色方块，但是却无法走到这些位置，因此最终可以走通的位置应该如下图。

代码

/**
 * @param {number} m
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var movingCount = function (m, n, k) {
  let step = {};
  let num = 0;
  function dfs(i, j) {
    if (i < 0 || j < 0 || i >= n || j >= m) return;
    if (!step[`${i}|${j}`] && canMove(i, j, k)) {
      step[`${i}|${j}`] = true;
      num++;

      dfs(i, j - 1);
      dfs(i - 1, j);
      dfs(i + 1, j);
      dfs(i, j + 1);
    }
  }
  dfs(0, 0);
  return num;
};

function canMove(i, j, k) {
  let valI = i
    .toString()
    .split("")
    .reduce((a, b) => {
      return Number(a) + Number(b);
    });
  let valJ = j
    .toString()
    .split("")
    .reduce((a, b) => {
      return Number(a) + Number(b);
    });
  if (Number(valI) + Number(valJ) <= k) {
    return true;
  }
  return false;
}

// 使用set的特性，记录符合条件的格子
/**
 * @param {number} m
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var movingCount = function (m, n, k) {
  const sumOfDigits = (num) => {
    let sum = 0;
    while (num > 0) {
      const temp = parseInt(num / 10);
      sum += num % 10;
      num = temp;
    }
    return sum;
  };
  const step = new Set();
  const dfs = (i, j, k) => {
    if (
      i < 0 ||
      i >= m ||
      j < 0 ||
      j >= n ||
      sumOfDigits(i) + sumOfDigits(j) > k ||
      step.has(`${i},${j}`)
    )
      return;
    step.add(`${i},${j}`);
    dfs(i + 1, j, k);
    dfs(i, j + 1, k);
  };

  dfs(0, 0, k);
  return step.size;
};

参考

面试题 13. 机器人的运动范围