1162. 地图分析
题目描述
你现在手里有一份大小为 N x N 的『地图』(网格) grid,上面的每个『区域』(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,你知道距离陆地区域最远的海洋区域是是哪一个吗?请返回该海洋区域到离它最近的陆地区域的距离。
我们这里说的距离是『曼哈顿距离』( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。
如果我们的地图上只有陆地或者海洋,请返回 -1。
你现在手里有一份大小为 N x N 的『地图』(网格) grid,上面的每个『区域』(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,你知道距离陆地区域最远的海洋区域是是哪一个吗?请返回该海洋区域到离它最近的陆地区域的距离。
我们这里说的距离是『曼哈顿距离』( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。
如果我们的地图上只有陆地或者海洋,请返回 -1。
示例
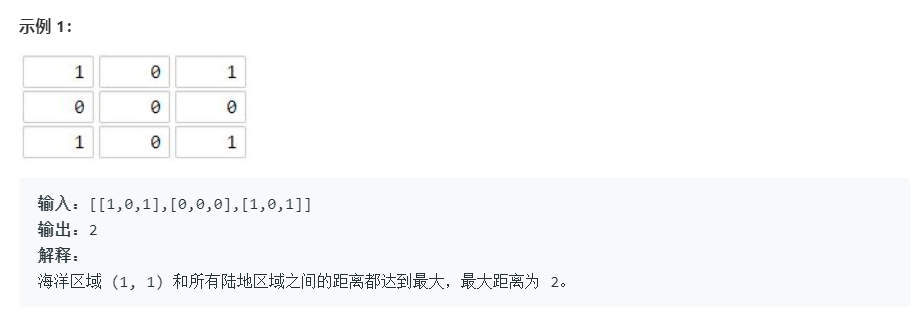
解题思路
分析
「离陆地区域最远」要求海洋区域距离它最近的陆地区域的曼哈顿距离是最大的。所以我们需要找一个海洋区域,满足它到陆地的最小距离是最大的。
方法一:暴力求解
最简单的办法,即求出每一个海洋区域(grid[i][j] == 0 的区域)的「最近陆地区域」,然后记录下它们的距离,然后在这些距离里面取一个最大值。
代码:
var maxDistance = function(grid) {
let land = [];
let ocean = [];
//记录 陆地和海洋
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid.length; j++) {
if (grid[i][j]) {
land.push([i, j]);
} else {
ocean.push([i, j]);
}
}
}
// 全是海洋和陆地的情况
if (land.length === 0 || ocean.length === 0) {
return -1;
}
//求每一个海洋区域跟所有陆地的最小距离,
let max = 0;
for (let i = 0; i < ocean.length; i++) {
//求一片海洋到所有陆地的距离中最小的距离
let min = 9999;
for (let j = 0; j < land.length; j++) {
const dis = distance(ocean[i], land[j]);
min = min < dis ? min : dis;
if (min === 1) {
break;
}
}
//求最小距离中的最大距离
max = max > min ? max : min;
}
return max;
};
/**
* 曼哈顿距离
* @param a
* @param b
* @returns {number}
*/
function distance(a, b) {
return Math.abs(a[0] - b[0]) + Math.abs(a[1] - b[1]);
}方法二:动态规划
将初始陆地坐标放进队列,然后逐次取出队列坐标,判断其上下左右是否有海洋,有则将海洋的值改为 1,放进队列,第一轮结束后距离加 1;之后每轮都是一样的操作,直至队列没有元素.在判断陆地周围是否有海洋的时候按照如下四个方向:
- (x - 1, y)(x−1,y)
- (x, y + 1)(x,y+1)
- (x + 1, y)(x+1,y)
- (x, y - 1)(x,y−1)
代码
/**
* @param {number[][]} grid
* @return {number}
*/
var maxDistance = function(grid) {
let [land, maxDistance] = [[], -1];
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
// 构建陆地数组
if (grid[i][j]) land.push([i, j]);
}
}
// 全是海洋或者陆地,返回-1
if (land.length == (0 || grid.length * grid[0].length)) return -1;
while (land.length != 0) {
let len = land.length;
for (let k = 0; k < len; k++) {
let [i, j] = land.shift();
// 对于每一个陆地,判断四个方向,将四个方向上的海洋置为1
if (i > 0 && grid[i - 1][j] == 0) {
grid[i - 1][j] = 1;
land.push([i - 1, j]);
}
if (i < grid.length - 1 && grid[i + 1][j] == 0) {
grid[i + 1][j] = 1;
land.push([i + 1, j]);
}
if (j > 0 && grid[i][j - 1] == 0) {
grid[i][j - 1] = 1;
land.push([i, j - 1]);
}
if (j < grid[0].length - 1 && grid[i][j + 1] == 0) {
grid[1][j + 1] = 1;
land.push([1, j + 1]);
}
}
maxDistance++;
}
return maxDistance;
};
